Cuadratura segundo Specht
 |
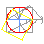
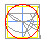
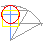
Segue o cálculo de p Constrúese un triángulo rectángulo que ten como catetos 11/10 e 1/2 do raio. << Pasar o cursor por enriba do gráfico |
Cuadratura segundo
o cálculo xeométrico de |
 |
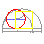            |
Cuadratura segundo Specht
 |
Segue o cálculo de p Constrúese un triángulo rectángulo que ten como catetos 11/10 e 1/2 do raio. << Pasar o cursor por enriba do gráfico |
Cuadratura segundo
o cálculo xeométrico de |
 |
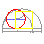            |