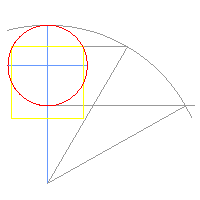
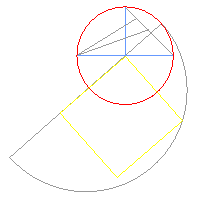
Colección de aproximacións gráficas á
Cuadratura do Círculo

  

Construir un cadrado equivalente en superficie a un círculo dado

Métodos ordenados pola exactitude do resultado

Cuadratura exipcia I
Cuadratura exipcia II
Cuadratura babilónica
aproximación: 0,0189.r
aproximación: 0,0189.r
aproximación: 0,016.r
     
Pi = 2 + 3
Cuadratura pola raiz do número áureo I
Cuadratura pola raiz do número áureo II
aproximación: 0,004672.r
aproximación: 0,003.r
aproximación: 0,003.r
 
Cuadratura polo número áureo
Cuadratura pola raiz de 2
Cuadratura de Kochansky,
pola tanxente de 30º
aproximación: 0,001.r
aproximación: 0,00038.r
aproximación: 0,00006.r
     
Cuadratura polo cadrado do número áureo I
Cuadratura polo cadrado do número áureo II
 Cuadratura de Viète
aproximación: 0,00005.r
aproximación: 0,00005.r
 aproximación: 0,00005.r
 
Cuadratura de Hobson Cuadratura Pitagórica Cuadratura Pitagórico-salomónica
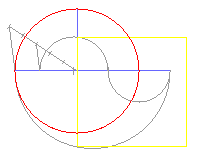aproximación: 0,00005.r aproximación: 0,00005.r

aproximación: 0,0000056.r
Cuadratura pola tanxente do ángulo de 40º Cuadratura segundo Goodhue Cuadratura segundo
Specht

aproximación: 0,000003.r

aproximación: 0,0000014.r

aproximación: 0,0000007.r
 
Cuadratura con 2/3 de raíz de cinco

Cuadratura segundo
Gelder

Cuadratura 1 de Ramanujan

aproximación: 0,00000037.r

aproximación: 0,0000003.r

aproximación: 0,00000027.r
Cuadratura pola raiz de 5 Cuadratura pola tanxente de 30º Cuadratura 1 de Frei Martín Sarmiento

aproximación: 0,00000015.r

aproximación: 0,000000055.r

aproximación: 0,0000000093.r
 
Cuadratura dos tres lados do decágono Cuadratura 2 de Ramanujan Cuadratura 2 de Frei Martín Sarmiento

aproximación: 0,0000000060.r

aproximación: 0,0000000010.r

aproximación: 0,000000000039.r