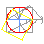
Cuadratura segundo Gelder
Construción proposta en 1849 por Jacob de Gelder (1808-1890), tomado de Delahaye, Jean-Paul: Le fascinant
nombre |
 |
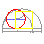       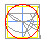 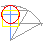    |
Cuadratura segundo Gelder
Construción proposta en 1849 por Jacob de Gelder (1808-1890), tomado de Delahaye, Jean-Paul: Le fascinant
nombre |
 |
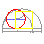            |