Cuadratura pola tanxente de 30º

 

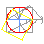
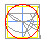
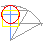
Seguindo o método de rectificación (1685) de Kochansky, constrúese un ángulo de 30º para restar a súa tanxente a un segmento triple do raio.

 

<< Pasar o cursor por enriba do gráfico


A hipotenusa do triángulo que o segmento resultante forma co diámetro aproxímase ao valor de .

A media proporcional entre e o raio é o lado do cadrado.

 

teórico 3,1415926
construido 3,1415333
erro = 0,00006.r
Método común, baseado na rectificación de Adam Kochansky (1631-1700)
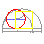Cuadratura exipcia (I) Cuadratura exipcia (II) cuadratura babilónica Cuadratura R2 + R3 Cuadratura pola raiz de fi (I) Cuadratura pola raiz de fi (II)Cuadratura polo número áureo Cuadratura pola raíz de 2 Cuadratura pola tanxente de 30º
Cuadratura polo cadrado do número áureo (I)Cuadratura polo cadrado do número áureo (II) Cuadratura de Viète Cuadratura de Hobson Cuadratura pitagorica Cuadratura pitagórico-salomónica Cuadratura pola tanxente de 40º Cuadratura de Goodhue Cuadratura de Specht
Cuadratura con 2/3 de raíz de 5 Cuadratura de Gelder Cuadratura 1 de Ramanujan Cuadratura pola raiz de 5 Cuadratura pola tanxente de 30º Cuadratura 1 de Sarmiento Cuadratura dos tres lados do decágono Cuadratura 2 de Ramanujan Cuadratura 2 de Sarmiento