
PROPORCIÓN, RECTÁNGULOS E FORMATOS
En calquera das civilizacións antigas buscuse a perfección das formas na relación de medidas que vinculaban as distintas partes da obra, cada parte co total, o total co formato-soporte e mesmo as do soporte en si.
O termo que empregaron os gregos foi Simetria, pero como hoxe esa palabra pasou a referirse a outra cousa distinta, concretamente a equidistancia de dous elementos a un centro ou eixo en sentido inverso, pois as relacións de medida estúdianse como Proporción, e é un campo fundamental dentro da Composición.
Hai dous tipos de proporción xeométrica:
1- a que establece entre dous elementos unha razón sinxela, expresable
como dous múltiplos dunha unidade ou módulo: 2/3, 3/5, 1/2 (proporción
estática)
2- a que relaciona dous valores por unha razón inconmensurable, como
un radical: de 2, de 3, de 5, número pi, razón áurea,
etc. (proporción dinámica)
Os pitagóricos e o platonismo en xeral estudaron exaustivamente as razóns estáticas cando matemáticas e xeometría estaban en cueiros. Vincularon estas razóns aos intervalos consonantes na música, onde o unísono é a razón 1:1, a octava 1:2, a quinta (do-sol) 2:3, a cuarta (do-fa) 3:4, a terceira maior (do-mi) 4:5, etc. Compóebase perfectamente nun monocordio ou ben nunha guitarra, onde o traste 12 está xusto no punto medio da lonxitude da corda, o 7º nos 2/3, o 5º nos 3/4 etc, sempre por orde en calidade armónica.

A música, de carácter unidimensional, réxese polas razóns sinxelas, aínda que compositores contemporáneos teñen experimentado razóns inconmensurables, en especial na súa dimensión temporal (ritmos). Nas artes visuais as razóns musicais rexen estructuras modulares, mentras que as razóns dinámicas dan un carácter espacial máis aberto.
A figura humana e as fachadas de edificios foron dous temas clave na aplicación de razóns proporcionais. Cando non había fotografía había que construír a figura, e neste empeño temos exemplos de todo tipo:
Sistemas modulares, baseados na repetición dunha unidade ou módulo: pinturas e relevos exipcios, tratadistas como Arfe y Villafañe, Irala, etc.
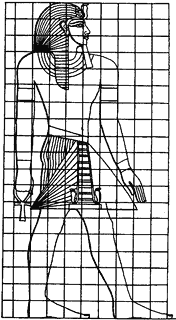

Sistemas que establecen cada parte como unha fracción da altura: Vitrubio, Durero, Pacheco, e en xeral todos os tratados que dividen a altura en 8 cabezas, 10 caras, 6 pes, etc.

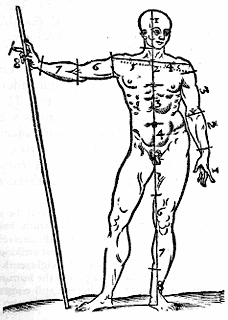
Esquemas simbólicos, de adaptación a formas xeométricas: Villard de Honnecourt, Bizancio, canon Varrónico.


Sistemas de analoxías e equivalencias na estructura: cánones gregos, antropometría moderna.


Aplicación da razón áurea: da Vinci, Zeising, Theodore Cook, Le Corbusier.


En fotografía, onde o modelo non se construe, senón que se capta a partir de certo punto de vista, baixo certo ángulo e encadre, e onde o resultado adoita ser unha imaxe contida nun espacio rectangular, interesa entender a proporción do formato.
O cadrado representa a unidade, o unísono. Ten moita forza visual, pero é a forma rectangular máis estática. No resto dos rectángulos domina o ancho ou o alto, así que participan das propiedades expresivas da dirección horizontal e da vertical. Como queira que a horizontal é a dimensión do tempo, da constancia, da estabilidade, da pasividade, os formatos apaisados reforzan nas paisaxes a sensación de placidez, de intemporalidade, mentras que os verticais poden suliñar temas máis activos e comunicativos, como o retrato, a figura ou o movemento vertical de por exemplo unha cascada.

Os formatos modulares ou estáticos resúltannos cómodos perceptivamente. Están baseados en razóns aritméticas sinxelas:

Algúns rectángulos dinámicos interesantes son: o rectángulo raiz de 2, que se obtén abatindo a diagonal dun cadrado, o raíz de 3, que se inscribe nun hexágono regular, ou o rectángulo áureo, que se obtén abatindo a "diagonal" da metade do cadrado:

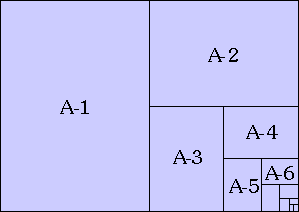
O rectángulo áureo merece un artículo aparte. O raiz de 2 tamén é importante a nivel práctico porque resolve o problema da duplicación mantendo as proporcións. Se dividimos un cadrado en dous rectángulos iguais, está claro que éstas xa non manteñen a forma cadrada. Isto sucede en calquera rectángulo estático. Sen embargo as dúas metades dun raiz de 2 teñen esta mesma proporción. A serie DIN-A normalizou os formatos de papel a partir dun rectángulo dun metro cadrado de superficie cos seus lados en proporción 1 a raíz de 2, que é o formato A-0. a súa metade é o formato A-1, a metade deste é o A-2, a metade deste A-3, e así co A-4 que sustitue os tradicionais formatos arbitrarios de folio, o A-5 que sustitue a cuartilla, o A-6 a octavilla, etc. etc.
Os fotogramas dun negativo de 35mm son rectángulos estáticos, de formato 2/3. Son idóneos para imprimir copias de 15x10 cm. pero cando queremos unha copia do duplo de superficie atopámonos cun rectángulo de 3x4, co que se produce un desfase que só se soluciona deixando unha marxe en branco (A) ou recortando parte da foto (B). O mesmo problema temos cunha dixital que fai fotos en formato 3x4 se queremos revelar en 15x10 cm (C), e con calquera cámara se imos a un tamaño poster de 70x50.

Os subministros de papel fanse con mentalidade rigurosamente estática, os cortes son sempre en múltiplos de 5 cm., con excepcións tan raras como o formato 13x18 cm, tan irregular porque vén do costume de recortar copias de 20x15 para poñelas en marcos de 13 x 18, que miden así porque se fabricaban para poñerlle a unha copia estándar de 15 x 10 un passe-partout de 15mm.
O formato raíz de 2 é o que permite ampliar ao duplo de superficie nunha fotocopiadora un documento sen ter que facer axustes nin recortes, por iso nas máquinas sempre están os valores de raíz de 2 e o seu inverso: 141% e 71%. ¿Chegará un día en que se resolva o problema cos formatos de copia estándar? parece difícil, xa non servirían os albuns antigos, os marcos antigos, os sensores e películas antigas...