O seu nome ten algo de mítico porque soa moito máis do que realmente é coñecida. Tamén se lle chama divina proporción, número de ouro, regra dourada, etc. A súa construcción e uso non é nada complicado, o que pasa é que resulta moito máis inmediato facer unha proporción estática, baseada na igualdade, como dividir algo por un número enteiro, o mesmo que establecer un ritmo de crecemento a partir de por exemplo a duplicación: 1, 2, 4, 8, 16... No mundo da informática é o usual, e cando nos condicionan factores materiais, espaciais, físicos, a cuadrícula é a forma máis cómoda de adaptarse a estes condicionantes. Sen embargo na natureza maniféstanse outras organizacións formais e principios proporcionais moito máis interesantes como modelo para o traballo criativo.

A proporción áurea está formulada xa nos Elementos de Euclides (s.-III), nunha construcción xeométrica denominada División dun segmento en media e extrema razón. A idea é tan sinxela como perfecta: O todo divídese en dúas partes tal que, a razón proporcional entre a parte menor e a maior, é igual á existente entre a maior e o total, é dicer, a suma de ambas as dúas.

O segmento de partida é AB. Para aplicarlle a Sección Áurea colócase perpendicularmente nun extremo (B) outro segmento que mida exactamente a metade. Defínese así un triángulo rectángulo cos catetos en proporción 1:2. Pois ben, á hipotenusa réstaselle o cateto menor (arco da dereita) e a diferencia, que levamos ao segmento AB con outro arco, é a sección áurea deste. A parte menor Bfi é á maior Afi como ésta é á suma AB.

Igual de sinxelo é facer a operación inversa, é dicer, averiguar de qué medida é sección áurea o segmento AB. Formamos o mesmo triángulo que antes, pero en lugar de restar á hipotenusa o cateto menor, súmanse. AB é sección áurea de Afi, e este segmento é a suma de AB e a súa sección áurea calculada no esquema anterior, por suposto.

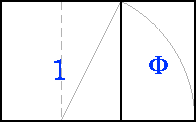
Un rectángulo áureo é aquel no que os lados están en razón áurea. Pódese construir rápidamente a partir dun cadrado: collemos o punto medio da base, tomamos cun compás a distancia até un dos vértices superiores e cun arco levamos esta medida á prolongación da base. O rectángulo ampliado é áureo, como también a ampliación, se suprimimos o cadrado inicial, ten esta mesma proporción:

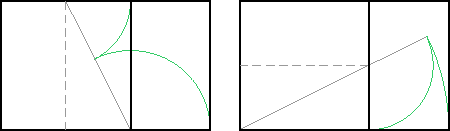
Ás veces vemos estas outras construccións, pero fan o mesmo que a anterior, definir un triángulo rectángulo cun lado e a metade doutro, restar a metade á hipotenusa e aplicar a diferencia como ampliación do cadrado:

A continuación comento algunhas curiosidades xeométricas, pero quen estea interesado só polo trazado e por facer algunha proba, pode saltar esta parte.

A (pseudo)espiral logarítmica
Do gráfico anterior, deducimos que a calquera rectángulo áureo se lle pode restar polo seu lado menor ou ben engadir polo seu lado maior un cadrado, e o resultado segue a ser un rectángulo áureo. En gnomónica diríamos que o cadrado é o gnomon do rectángulo áureo (traduzo: gnomon é aquela figura que engadida a outra aporta máis superficie sen cambiar a forma). Esta propiedade ilústrase frecuentemente con esta espiral logarítmica:

O de espiral logarítmica hai que matizalo, é una pseudo-espiral porque se forma con arcos de 90º de circunferencia inscritos en cada cadrado e enlazados entre si, mentras que nunha verdadeira espiral hai un cambio de curvatura constante, non cambios puntuais. Pero medra en proporción xeométrica, por iso o de logarítmica.

O seu valor numérico
Se facemos a construcción do rectángulo áureo cara os dous lados dun cadrado, o total é un rectángulo Raiz de cinco (os seus lados están en proporción 1:R5)

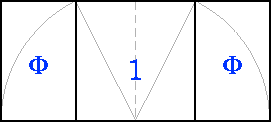
Vese aínda máis claro se poñemos un cadrado duplo. Polo Teorema de Pitágoras sabemos que a súa diagonal mide Raiz de 5, e é o duplo que o radio utilizado nas construccións anteriores. Así que realmente o que estábamos facendo con aquel triángulo era sumar ou restar 0'5 á hipotenusa que é 1/2 de R5.

A fórmula por tanto é fi = R5+1 / 2 = 1'61803398
E a súa inversa (sección áurea) fi = R5-1 / 2 = 0'61803398
Vese perfectamente que forman unha serie aditiva, porque entre os dous valores está o factor 1.

Fibonacci
A relación desta proporción con Leonardo de Pisa, máis coñecido por Fibonacci (s.XVI) é que éste matemático indicou aos criadores de coellos a conveniencia de prever a producción calculando as cantidades de exemplares en series aditivas: cada mes unha parella produce como media dúas crías, que ao mes seguinte xa poden procrear, como tamén a parella inicial. Así que cada previsión é a suma da anterior máis a súa producción. A estas series, nas que cada termo é a suma dos dous anteriores, chámaselles dende entón series de Fibonacci. Pois ben, resulta que o límite de calquera destas series é a razón áurea: 1,618033989. É dicer, tomamos dous números calquera como 2 e 6. Se comezamos unha serie os seguintes termos serían 8, 14, 22, 36, etc. Se observamos a razón entre cada termo e o anterior, veremos que comeza en 3, segue en 4/3, e vai oscilando aproximándose cada vez máis a un valor que en 7 ou 8 pasos xa é indistinguible de 1,618
En todo caso, a progresión en razón áurea é a única que reúne dúas características: ser serie de Fibonacci (aditiva) e xeométrica. Cada termo é a suma dos dous anteriores e é media proporcional entre o anterior e o seguinte.

O seu nome e nomenclatura
A Divina Proporción é o título dun tratado sobre as propiedades desta razón e a súa presencia nos poliedros regulares, debido a Fra Luca Pacioli, co interés engadido de que a obra estivo ilustrada por Leonardo da Vinci. No século XIX e primeiros do XX houbo un interés moi grande por esta proporción, e dende entón é habitual indicala coa legra grega fi, uns din que en homenaxe a Fidias e outros que en relación con Fibonacci.
En orde crecente, dise que cada termo é "sección" áurea do seguinte, mentras que o valor nominal fi é o factor de progresión 1,618. Así que a mellor maneira para non se trabucar é esta:

A súa relación co pentágono e dodecágono regulares
Comentéi nalgún artigo anterior que hai tres grandes familias xeométricas, rexidas por tres raíces: R2, R3 e R5. A R2 regula a estructura do cadrado, a duplicación. R3 rexe as propiedades do triángulo equilátero e o hexágono. En base a calquera das dúas podemos organizar en rede todo o plano, resolvendo o que comentaba antes, de "acatar" as limitacións físicas

A terceira familia, de Raíz de 5, a proporción áurea e o pentágono, non ofrece utilidades inmediatas, con ela é imposible xerar estructuras isótropas que cubran todo o espacio. Non se accede ás súas propiedades por simples deducción visual, senón a costa dunha observación activa, intencionada. Dende a admiración dos pitagóricos polo pentágono estrelado até a construcción de cúpulas xeodésicas derivadas do icosaedro, sempre tivo ese carácter oculto, contemplativo, abstracto, tan atractivo para os amantes da xeometría e as matemáticas.
Mais por outra banda, é un sistema moi compacto; aló onde aparece está en todas partes. Para construir o pentágono regular, ben a partir do lado base, ben circunscrito nunha circunferencia, sempre temos que recorrer á proporción áurea: vese claramente que as operacións son as mesmas que vimos antes:

Isto é porque todos os elementos están relacionados entre sí por esta proporción:

A- O lado é sección áurea da diagonal.
B- Cada diagonal divide a outras dúas segundo a sección áurea.
C- Se facemos un rectángulo áureo co radio r como lado maior, a diagonal é igual ao lado do pentágono, e o lado menor igual ao lado do decágono.

D- Se facemos un rectángulo áureo co radio r como lado menor, a diagonal mide igual que a diagonal do pentágono.
E- O radio é sección áurea do diámetro da circunferencia inscrita, que é o duplo da apotema.
F- A altura h do pentágono mide R5 en relación á apotema.

O Pentagrama pitagórico
Os pitagóricos adoptaron como símbolo o Pentágono regular estrelado. Tamén se lle chamou Pentagrama ou Pentalfa (cinco puntas en forma de alfa). Á parte da simboloxía do seu número, a súa propiedade xeométrica é que todos os segmentos están en progresión áurea.

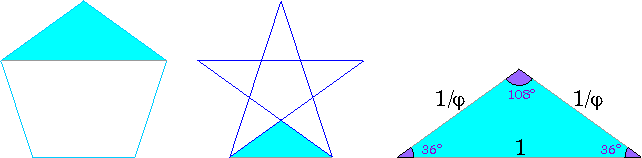
O triángulo do pentalfa, tamén chamado Triángulo Sublime e Triángulo áureo maior, ten os seus lados en proporción áurea, e os seus ángulos en razón sinxela 1:2:2. Aparece en diversas formas no pentágono e no decágono:

O seu complementario, o Triángulo Divino ou Triángulo áureo menor, tamén é isósceles, tamén ten os seus lados en proporción áurea, e os seus ángulos en razón sinxela 3:1:1. Aparece no Pentágono:

De feito, se dividimos un pentágono usando vértices e cruces de diagonais sempre resultará descomposto en varios triángulos de ambos os dous tipos. Se partimos un destes triángulos dende un vértice á sección áurea do lado contrario, a división dará un triángulo de cada tipo. Á inversa, adosando a un deles o contrario, pódese agrandar a superficie do primeiro. Polo tanto, cada un é gnomon do outro.

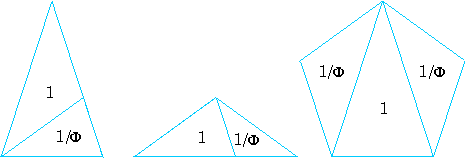
As superficies dos triángulos así divididos gardan a proporción áurea. A superficie do Pentágono regular, como vemos na última figura, é R5 veces a do triángulo central. A proporción maniféstase en todas as partes, como un sistema perfectamente coherente.

A súa presencia no Dodecaedro e no Icosaedro
Entre os sólidos platónicos, estes dous participan da proporción áurea en diversas cousas. Por exemplo, no Dodecaedro, a arista é sección áurea da diagonal de cara, e ésta éo da distancia entre aristas opostas. Se o colocamos sobre unha cara, as alturas dos vértices intermedios seccionan en sentido alterno a altura total. Visto dende enriba, os radios das circunferencias que pasan polos vértices das bases e polos vértices intermedios, están en razón áurea.

No Icosaedro podemos inscreber tres rectángulos áureos perpendiculares entre si, o que significa que a arista é sección áurea da distancia entre aristas opostas. Se o colocamos sobre un vértice, os tramos das alturas seguen a razón áurea, como tamén, visto dende enriba sobre unha cara, os radios das circunferencias que pasan polos vértices das bases e polos vértices intermedios.